超级码力在线编程大赛初赛 第2场 题解
下面的题解仅代表个人观点，出了问题，概不负责。
比赛链接：https://tianchi.aliyun.com/oj/15165469968503404?spm=5176.15098393.J_6210563800.8.6b8b5cd6dK6WtT
1. 三角魔法
描述
小栖必须在一个三角形中才能施展魔法，现在他知道自己的坐标和三个点的坐标，他想知道他能否施展魔法
- −109<=x,y<=109
- 点在边上也属于三角形内
示例
输入: triangle = [[0,0],[2,0],[1,2]] point= [1,1]
输出: "Yes"
输入: triangle = [[0,0],[2,0],[1,1]] point= [2,1]
输出: "No"
思路
判断是否在三角形内，模板题。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
|
class Vector2d
{
public:
double x_;
double y_;
public:
Vector2d(double x, double y) : x_(x), y_(y) {}
Vector2d() : x_(0), y_(0) {}
//二维向量叉乘, 叉乘的结果其实是向量，方向垂直于两个向量组成的平面，这里我们只需要其大小和方向
double CrossProduct(const Vector2d vec)
{
return x_ * vec.y_ - y_ * vec.x_;
}
//二维向量点积
double DotProduct(const Vector2d vec)
{
return x_ * vec.x_ + y_ * vec.y_;
}
//二维向量减法
Vector2d Minus(const Vector2d vec) const
{
return Vector2d(x_ - vec.x_, y_ - vec.y_);
}
//判断点M,N是否在直线AB的同一侧
static bool IsPointAtSameSideOfLine(const Vector2d &pointM, const Vector2d &pointN,
const Vector2d &pointA, const Vector2d &pointB)
{
Vector2d AB = pointB.Minus(pointA);
Vector2d AM = pointM.Minus(pointA);
Vector2d AN = pointN.Minus(pointA);
//等于0时表示某个点在直线上
return AB.CrossProduct(AM) * AB.CrossProduct(AN) >= 0;
}
};
//三角形类
class Triangle
{
private:
Vector2d pointA_, pointB_, pointC_;
public:
Triangle(Vector2d point1, Vector2d point2, Vector2d point3)
: pointA_(point1), pointB_(point2), pointC_(point3)
{
//todo 判断三点是否共线
}
//计算三角形面积
double ComputeTriangleArea()
{
//依据两个向量的叉乘来计算，可参考http://blog.csdn.net/zxj1988/article/details/6260576
Vector2d AB = pointB_.Minus(pointA_);
Vector2d BC = pointC_.Minus(pointB_);
return fabs(AB.CrossProduct(BC) / 2.0);
}
bool IsPointInTriangle1(const Vector2d pointP)
{
double area_ABC = ComputeTriangleArea();
double area_PAB = Triangle(pointP, pointA_, pointB_).ComputeTriangleArea();
double area_PAC = Triangle(pointP, pointA_, pointC_).ComputeTriangleArea();
double area_PBC = Triangle(pointP, pointB_, pointC_).ComputeTriangleArea();
if (fabs(area_PAB + area_PBC + area_PAC - area_ABC) < 0.000001)
return true;
else
return false;
}
bool IsPointInTriangle2(const Vector2d pointP)
{
return Vector2d::IsPointAtSameSideOfLine(pointP, pointA_, pointB_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointB_, pointA_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointC_, pointA_, pointB_);
}
bool IsPointInTriangle3(const Vector2d pointP)
{
Vector2d AB = pointB_.Minus(pointA_);
Vector2d AC = pointC_.Minus(pointA_);
Vector2d AP = pointP.Minus(pointA_);
double dot_ac_ac = AC.DotProduct(AC);
double dot_ac_ab = AC.DotProduct(AB);
double dot_ac_ap = AC.DotProduct(AP);
double dot_ab_ab = AB.DotProduct(AB);
double dot_ab_ap = AB.DotProduct(AP);
double tmp = 1.0 / (dot_ac_ac * dot_ab_ab - dot_ac_ab * dot_ac_ab);
double u = (dot_ab_ab * dot_ac_ap - dot_ac_ab * dot_ab_ap) * tmp;
if (u < 0 || u > 1)
return false;
double v = (dot_ac_ac * dot_ab_ap - dot_ac_ab * dot_ac_ap) * tmp;
if (v < 0 || v > 1)
return false;
return u + v <= 1;
}
bool IsPointInTriangle4(const Vector2d pointP)
{
Vector2d PA = pointA_.Minus(pointP);
Vector2d PB = pointB_.Minus(pointP);
Vector2d PC = pointC_.Minus(pointP);
double t1 = PA.CrossProduct(PB);
double t2 = PB.CrossProduct(PC);
double t3 = PC.CrossProduct(PA);
return t1 * t2 >= 0 && t1 * t3 >= 0;
}
};
class Solution
{
public:
/**
* @param triangle: Coordinates of three points
* @param point: Xiaoqi's coordinates
* @return: Judge whether you can cast magic
*/
string castMagic(vector<vector<int>> &triangle, vector<int> &point)
{
Triangle tri(Vector2d(triangle[0][0], triangle[0][1]),
Vector2d(triangle[1][0], triangle[1][1]),
Vector2d(triangle[2][0], triangle[2][1]));
return tri.IsPointInTriangle3(Vector2d(point[0], point[1])) ? "Yes" : "No";
}
};
|
2. 区间异或
描述
有一个数组num，现在定义区间对的和等于：左区间的最大值加右区间的最小值 由于小栖特别能突发奇想，他突然想知道多个区间对和的异或和是多少
- 4<=len(num)<=50000
-
- 1<=len(ask)<=100000
- len(ask[0])=4,分别表示 l1,r1,l2,r2
- num中视作下标从1开始，而不是0
- 左右区间可能重合
示例
输入: num = [1,2,3,4,5] ask = [[1,2,3,4],[1,2,4,5]]
输出: 3
说明: [1,2,3,4]区间异或对和为5，[1,2,4,5]区间异或对和为6，5 xor 6 = 3
思路
求区间最值，用线段树和RMQ都能搞，我用的RMQ
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
typedef long long ll;
#define N 100010
ll maxx[N][20];
ll minn[N][20];
void RMQ(ll n)
{
for (ll j = 1; j < 20; j++)
for (ll i = 1; i <= n; i++)
if (i + (1 << j) - 1 <= n)
{
maxx[i][j] = max(maxx[i][j - 1], maxx[i + (1 << (j - 1))][j - 1]);
minn[i][j] = min(minn[i][j - 1], minn[i + (1 << (j - 1))][j - 1]);
}
}
ll get_max(ll a, ll b)
{
ll k = (ll)(log(b - a + 1.0) / log(2.0));
return max(maxx[a][k], maxx[b - (1 << k) + 1][k]);
}
ll get_min(ll a, ll b)
{
ll k = (ll)(log(b - a + 1.0) / log(2.0));
return min(minn[a][k], minn[b - (1 << k) + 1][k]);
}
class Solution
{
public:
/**
* @param num: array of num
* @param ask: llerval pairs
* @return: return the sum of xor
*/
int Intervalxor(vector<int> &num, vector<vector<int>> &ask)
{
for (ll i = 0; i < num.size(); i++)
{
minn[i + 1][0] = maxx[i + 1][0] = num[i];
}
ll n = num.size();
RMQ(n);
ll ans = 0;
for (vector<int> as : ask)
{
ll l1 = as[0], r1 = as[1];
ll l2 = as[2], r2 = as[3];
ll tmp = get_max(l1, r1) + get_min(l2, r2);
ans ^= tmp;
}
return ans;
}
};
|
3. 五子回文
描述
小栖最近很喜欢回文串，由于小栖的幸运数字是5，他想知道形似“abcba"的回文串在他给定的字符串中的数量
- s.length<=106
- 字符串s只包含小写字母
示例
样例 1：
输入：s = "abcba"
输出：1
样例 2：
输入：s = "abcbabcccb"
输出：2
解释：形似”abcba“的字符串有”abcba“和”cbabc“
思路
直接O(n)遍历判断，不用算法。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution
{
public:
/**
* @param s: The given string
* @return: return the number of Five-character palindrome
*/
int pd(string &s, int mid)
{
bool f1 = s[mid - 1] == s[mid + 1];
bool f2 = s[mid - 2] == s[mid + 2];
bool f3 = (s[mid - 1] != s[mid - 2]) & (s[mid] != s[mid - 2]) & (s[mid] != s[mid - 1]);
return f1 & f2 & f3;
}
int Fivecharacterpalindrome(string &s)
{
int n = s.size();
if (n < 5)
return 0;
int ans = 0;
for (int i = 2; i < n - 2;)
{
if (pd(s, i))
{
i += 2;
ans++;
}
else
{
i++;
}
}
return ans;
}
};
|
4. 小栖的金字塔
描述
小栖有一个金字塔，每一层都有编号.
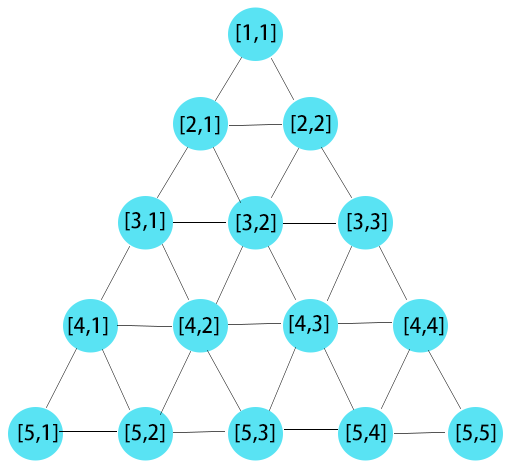小栖可以在不同点间移动，假设小栖现在在(x1,y1),他能够移动到的下一个点(x2,y2)满足x2>=x1&&y2>=y1x2>=x1&&y2>=y1 现在小栖呆在(k,k)处，由于我们不能确定小栖现在在哪儿，所以你需要求出所有点(k,k)到达(n,n)的方案数的和。
- 1<=k<=n<=107
- 由于方案数很大，请对方案数取模1e9+7
示例
输入：n=3,k=[1,2,3]
输出：9
思路
超级卡特兰数/大施罗德数 裸题。
题目中求的是 k 到 n 的方案数，所以对于每一个三角形而言，要求第 n-k+1 个大施罗德数。
模板可以看这里：https://blog.csdn.net/PleasantlY1/article/details/84074637
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
typedef long long LL;
const LL mod = 1e9 + 7;
const LL maxn = 1e7 + 10;
LL num[maxn];
LL inverse(LL x, LL y) ///快速幂加费马小定理求逆元
{
LL sum = 1;
while (y)
{
if (y & 1)
sum = sum * x % mod;
y /= 2;
x = x * x % mod;
}
return sum % mod;
}
class Solution
{
public:
/**
* @param n: The number of pyramid levels n
* @param k: Possible coordinates k
* @return: Find the sum of the number of plans
*/
int pyramid(int n, vector<int> &k)
{
num[1] = num[0] = 1;
for (int i = 2; i <= n; i++)
{
num[i] = ((6 * i - 3) * num[i - 1] % mod - (i - 2) * num[i - 2] % mod + mod) % mod * inverse(i + 1, mod - 2) % mod;
}
LL ans = 0;
for (auto x : k)
{
x = n - x + 1;
LL tmp = x == 1 ? 1 : num[x - 1] * 2 % mod;
ans = (ans + tmp) % mod;
}
return int(ans);
}
};
|
最后修改于 2020-08-30
本作品采用
知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。